LeetCode #22 — Generate Parentheses (Python)

Problem:

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

For example, given n = 3, a solution set is:

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

Approach: Recursion

After reading this question the first thing that I thought of was — how do I construct each string? And the answer to that can be broken down into 2 decisions— it was either adding a ‘(’ or ‘)’.

Taking the first item in the array above as an example — “((()))”. The decision process would be as follows:

Decision 1: append ‘(’ — Current String: ‘(’

Decision 2: append ‘(’ — Current String: ‘((’

… (you get the idea)…

Decision 5: append ‘)’ — Current String: ‘((())’

Decision 6: append ‘)’ — Current String: ‘((()))’

After realizing that each string can be constructed just from 2 decisions alone, the next thing to figure out was — How do I form all valid combinations?

For this, we need to recognize 2 limitations given the caveat of ‘well-formed’:

1. The total number of CP (closed parentheses) you have left to append at any given point in time cannot be lesser than the number of OP (open parentheses) available. For e.g. ‘(()))’ , ‘)’, ‘())’ are invalid for this reason.
2. When there is 0 OP left to use, you can only make 1 decision — append CP

With this in mind, here is the code

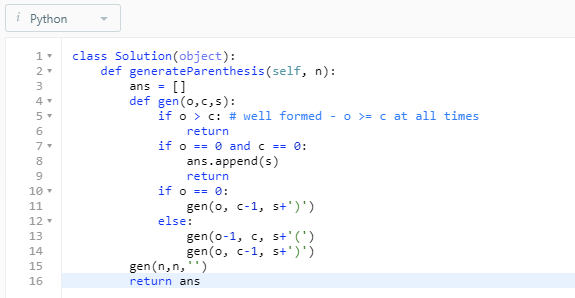
As you can see, ‘gen’ represents the recursive function. It takes in 3 parameters:

o — total no. of remaining OP available to append

c — total no. of remaining CP available to append

s — currently constructed string.

1st conditional statement — if o > c. Prevents limitation 1 from occurring. If this occurs, the function will simply stop calling itself recursively.

2nd conditional statement — if o==0 and c ==0. Event where a valid combination is formed with n specified OP and CP. When this occurs, the constructed string is appended to the ans arr.

3rd conditional statement — if o == 0.. else.., this portion of the recursive function determines how to continue with the recursive calls. In the case where OP is 0 (i.e. no more OP remaining to append), the only call to make (limitation 2), is to append a CP. The function then decreases the number of CP remaining by 1 and appends ‘)’ to the existing string s. Else, both decisions are made — decision to append ‘(’ and ‘)’.

I really hope someone found this helpful in some way or another. This probably isn’t the cleanest approach (code wise) to this question but the idea is there. Please leave a comment if there’s anything which needs clarification!